Authors: Wouter Saelens [aut, cre]
Version: 0.99.0
License: GPL-3
The triwise package provides function to analyze and visualize gene expression in three biological conditions. Gene expression is converted to a barycentric representation allowing the representation of each gene in a 2D plane.
R (>= 3.3), Biobase, BiocGenerics
htmlwidgets, Rcpp, mgsa, ggplot2, dplyr, MASS, RColorBrewer, jsonlite, plyr, scales
testthat, knitr, rmarkdown, BiocStyle, packagedocs, GSEABase, circular, tidyverse, cowplot, limma
Converts the expression matrix containing three biological conditions to barycentric coordinates, reducing its dimensionality by one while retaining information of differential expression.
transformBarycentric(E, transfomatrix = NULL)NULL (default) or a numeric matrix containing the transformation matrix
d-1 dimensions
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 1
barycoords = transformBarycentric(Eoi)
hist(barycoords$angle)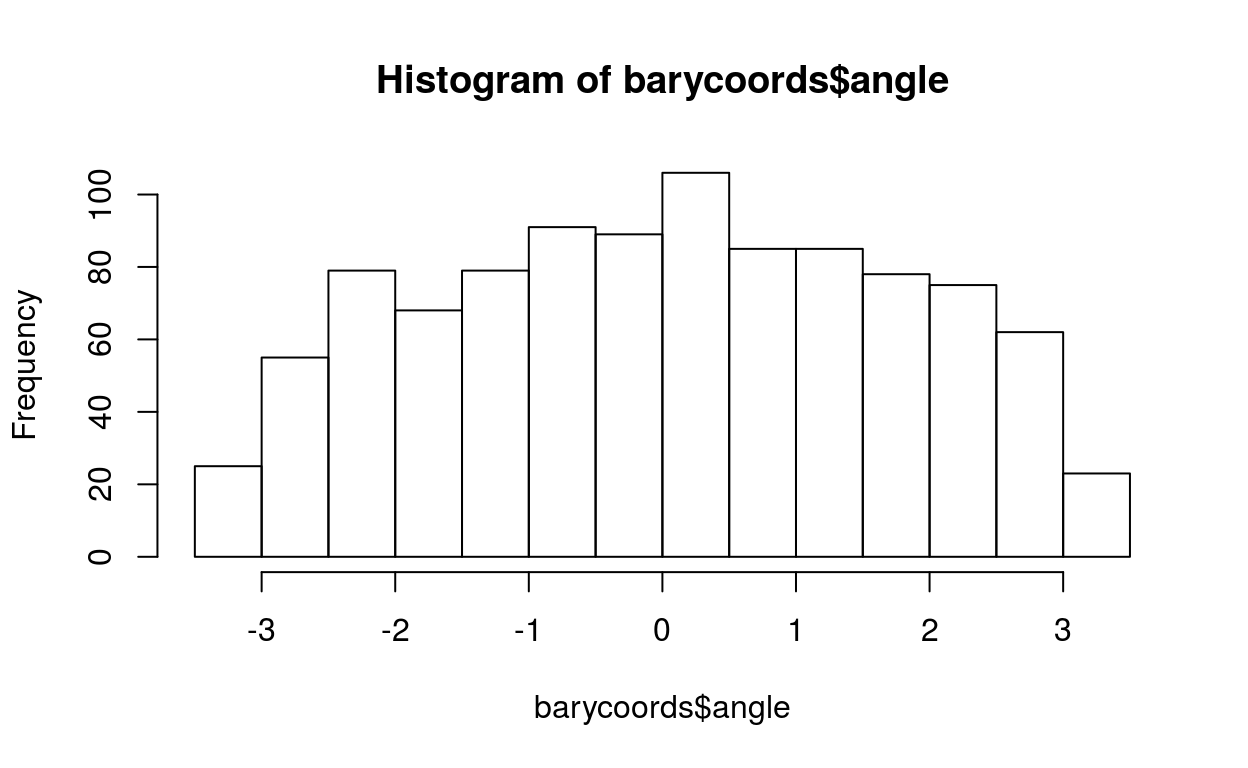
Converts a dataframe contain barycentric coordinates in the x and y columns back to original coordinates (apart from a constant for each gene).
transformReverseBarycentric(barycoords, transfomatrix = NULL)NULL (default) or a numeric matrix containing the transformation matrix
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 1
barycoords = transformBarycentric(Eoi)
reversebarycoords = transformReverseBarycentric(barycoords)
all.equal(scale(t(Eoi)), scale(t(reversebarycoords)), check.attributes=FALSE)## [1] TRUEGet the matrix for the barycentric transformation
getTransformationMatrix(anglebase = 0)
plot(t(getTransformationMatrix(0)), asp=1)
plot(t(getTransformationMatrix(pi/2)), asp=1)
plot(t(getTransformationMatrix(pi)), asp=1)
Plot a dotplot
plotDotplot(barycoords, Gdiffexp = rownames(barycoords), Goi = NULL, Coi = attr(barycoords, "conditions"), colorby = "diffexp", colorvalues = NULL, rmax = 5, showlabels = TRUE, sizevalues = stats::setNames(c(0.5, 2), c(FALSE, TRUE)), alphavalues = stats::setNames(c(0.8, 0.8), c(FALSE, TRUE)), barycoords2 = NULL, baseangle = 0)transformBarycentric
diffexp or nodiffexp). The second part denotes the name of the gene set. Genes not within a gene set are denoted by all. For example: list(diffexpall=“#000000”, nodiffexpall=“#AAAAAA”, nodiffexpgset=“#FFAAAA”, diffexpgset=“#FF0000”)
transformBarycentric. An arrow will be drawn from the coordinates in barycoords to those in barycoords2
data(vandelaar)
Eoi <- limma::avearrays(vandelaar, Biobase::phenoData(vandelaar)$celltype)
Eoi = Eoi[,c("YS_MF", "FL_mono", "BM_mono")]
barycoords = transformBarycentric(Eoi)
plotDotplot(barycoords)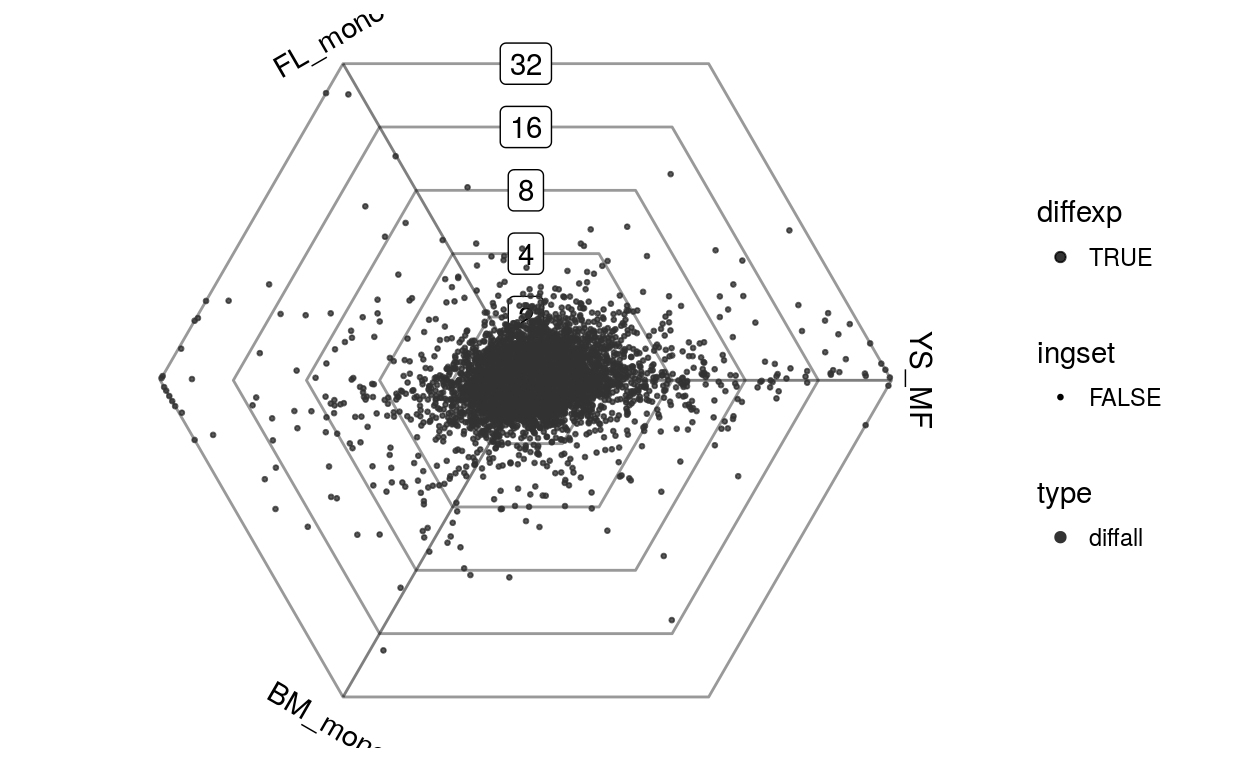
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 1
barycoords = transformBarycentric(Eoi)
Gdiffexp =(1:1000)[barycoords$r > 1]
plotDotplot(barycoords)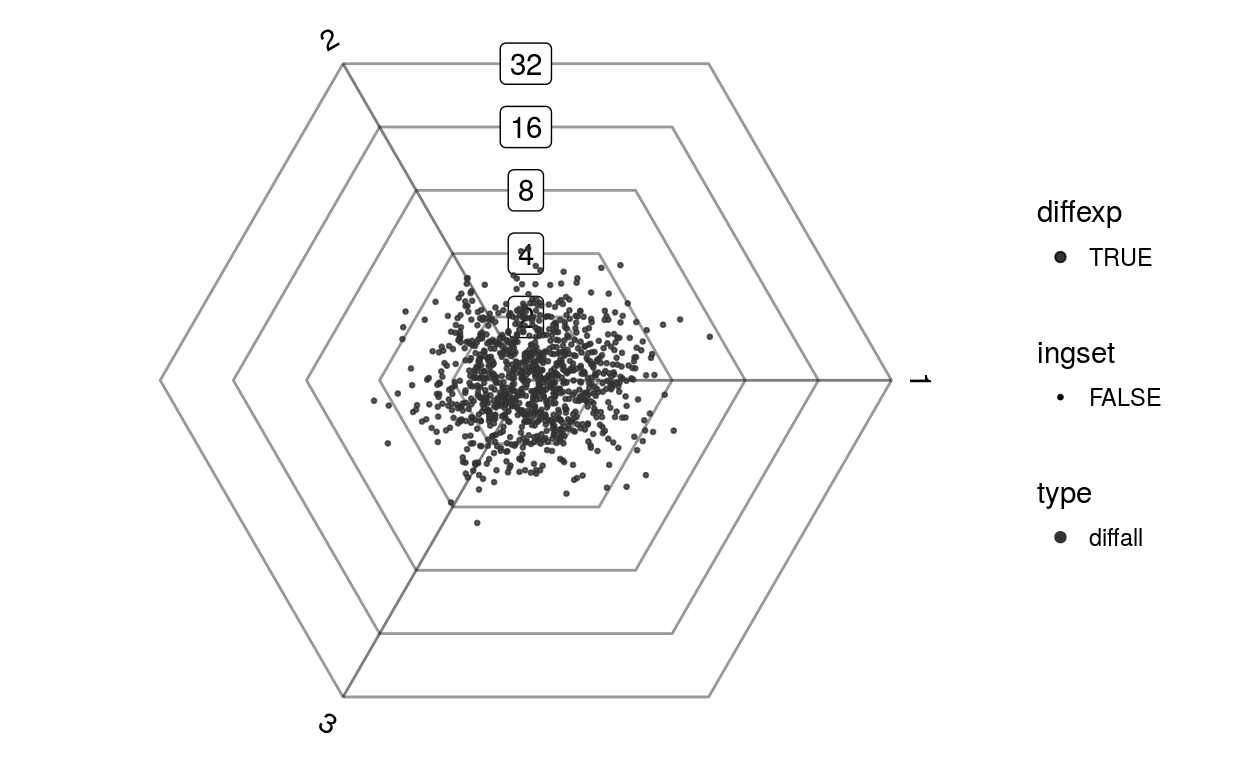
plotDotplot(barycoords, Gdiffexp)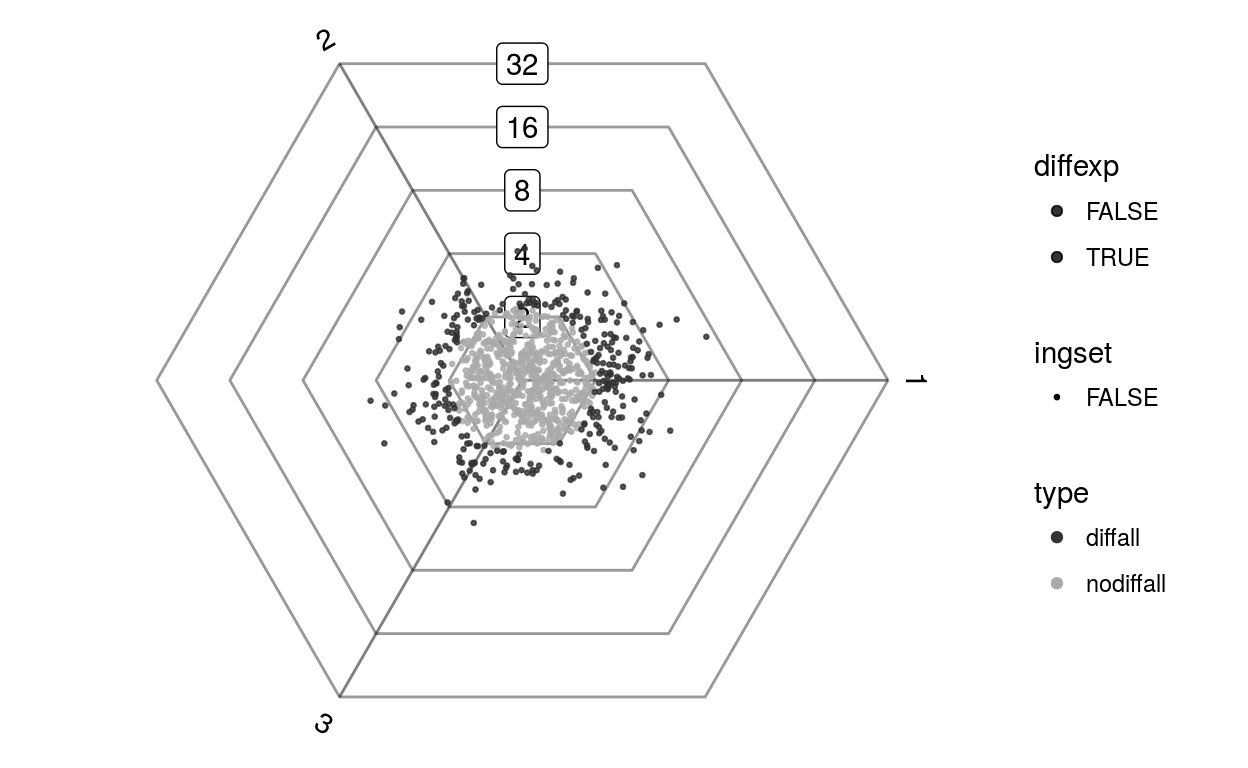
plotDotplot(barycoords, Gdiffexp, 1:100)
plotDotplot(barycoords, Gdiffexp, list(a=1:100, b=sample(100:1000, 50)))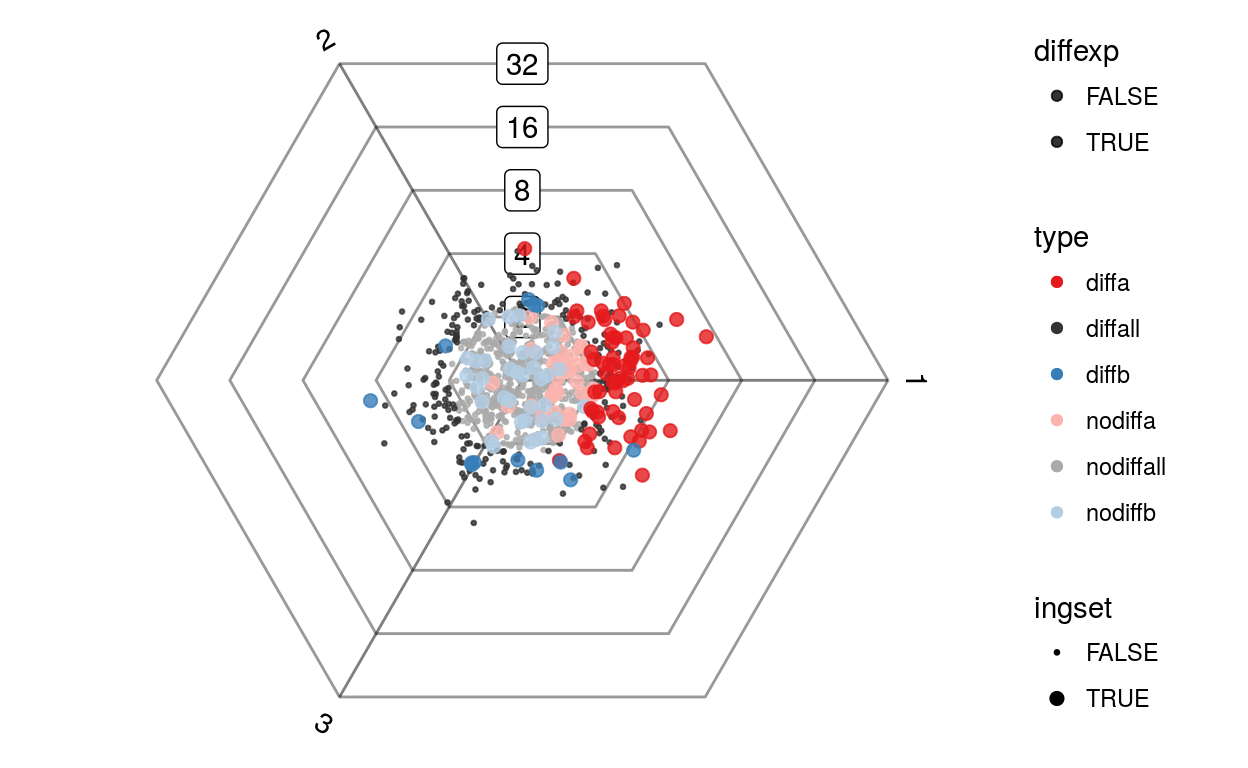
A rose plot shows the distribution of a given set of genes in different directions.
plotRoseplot(barycoords, Gdiffexp = rownames(barycoords), Goi = rownames(barycoords), size = "surface", relative = TRUE, showlabels = TRUE, Coi = attr(barycoords, "conditions"), nbins = 12, bincolors = grDevices::rainbow(nbins, start = 0, v = 0.8, s = 0.6), rmax = "auto", baseangle = 0)transformBarycentric.
radius or the surface of a circle sector denote the number of genes differentially expressed in a particular direction
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 1
barycoords = transformBarycentric(Eoi)
plotRoseplot(barycoords)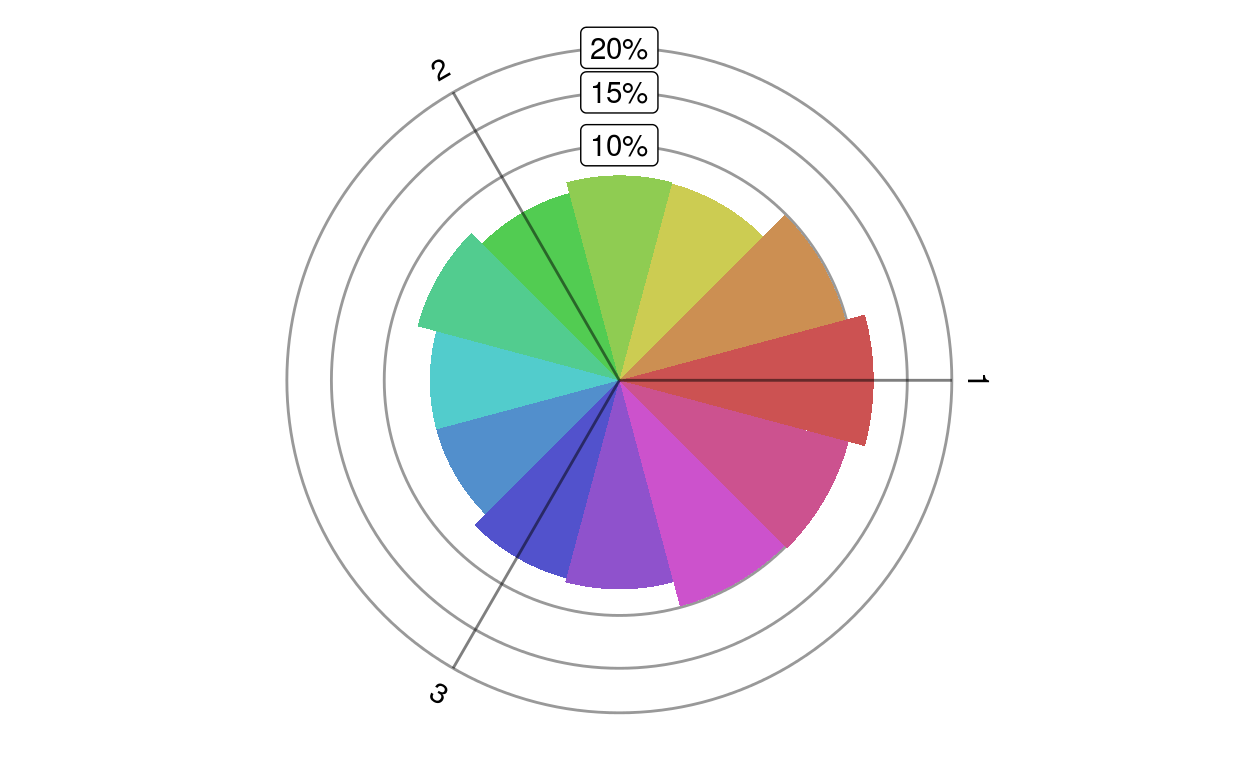
plotRoseplot(barycoords, (1:1000)[barycoords$r > 1])
plotRoseplot(barycoords, (1:1000)[barycoords$r > 1], 1:100)
Plots each enriched gene set as a dot on a dotplot
plotPvalplot(scores, Coi = c("", "", ""), colorby = NULL, showlabels = TRUE, baseangle = 0)testUnidirectionality containing for every gene set a q-value and an associated angle
scores used for coloring
0)
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 4 # the first 100 genes are more upregulated in the first condition
barycoords = transformBarycentric(Eoi)
gsets = list(a=1:50, b=80:150, c=200:500)
scores = testUnidirectionality(barycoords, gsets, Gdiffexp=(1:1000)[barycoords$r > 1])
plotPvalplot(scores)
Draw an interactive triwise dotplot using a html widget
interactiveDotplot(Eoi, Gdiffexp = rownames(Eoi), Goi = c(), Glabels = rownames(Eoi), Gpin = c(), Coi = colnames(Eoi), colorvalues = NULL, rmax = 5, sizevalues = c(`TRUE` = 2, `FALSE` = 0.5), alphavalues = c(`TRUE` = 0.8, `FALSE` = 0.8), plotLocalEnrichment = FALSE, width = NULL, height = NULL)Eoi
NULL will automatically choose the top 20 most differentially expressed genes
diffexp or nodiffexp). The second part denotes the name of the gene set. Genes not within a gene set are denoted by all. For example: list(diffexpall=“#000000”, nodiffexpall=“#AAAAAA”, nodiffexpgset=“#FFAAAA”, diffexpgset=“#FF0000”)
saveWidget
data(vandelaar)
Eoi <- limma::avearrays(vandelaar, Biobase::phenoData(vandelaar)$celltype)
Eoi = Eoi[,c("YS_MF", "FL_mono", "BM_mono")]
barycoords = transformBarycentric(Eoi)
## Not run:
# interactiveDotplot(barycoords)
# ## End(Not run)
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 1
barycoords = transformBarycentric(Eoi)
Gdiffexp =(1:1000)[barycoords$r > 1]
## Not run:
# interactiveDotplot(Eoi)
# interactiveDotplot(Eoi, Gdiffexp)
# interactiveDotplot(Eoi, as.character(Gdiffexp), as.character(1:10), as.character(1:1000))
# interactiveDotplot(Eoi, as.character(Gdiffexp), as.character(1:10), as.character(1:1000), c(50, 200))
# ## End(Not run)Draw a dotplot of p-values using a htmlwidget
interactivePvalplot(scores, gsetlabels, Coi, width = NULL, height = NULL)testUnidirectionality containing for every gene set a q-value and an associated angle
saveWidget
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 4 # the first 100 genes are more upregulated in the first condition
barycoords = transformBarycentric(Eoi)
gsets = list(a=1:50, b=80:150, c=200:500)
scores = testUnidirectionality(barycoords, gsets, Gdiffexp=(1:1000)[barycoords$r > 1])
## Not run:
# interactivePvalplot(scores, as.list(setNames(names(gsets), names(gsets))), 1:3)
# ## End(Not run)testUnidirectionality(barycoords, gsets, Gdiffexp = NULL, statistic = "diffexp", bm = NULL, minknown = 5, mindiffexp = 0, maxknown = 1500, mc.cores = getOption("mc.cores", default = 1), ...)transformBarycentric
generateBackgroundModel
generateBackgroundModel
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 4 # the first 100 genes are more upregulated in the first condition
barycoords = transformBarycentric(Eoi)
gsets = list(a=1:50, b=80:150, c=200:500)
testUnidirectionality(barycoords, gsets, Gdiffexp=(1:1000)[barycoords$r > 1])## pval angle n gsetid z qval
## 1 0.0000000000 0.01545295 50 a 0.98546551 0.0000000000
## 2 0.0004658351 0.03248947 71 b 0.31799432 0.0006987526
## 3 0.9927447804 5.92573169 301 c 0.02986189 0.9927447804
Generates a background model by randomly resampling genes at different n (number of genes) and angles and calculating z distributions
generateBackgroundModel(barycoords, noi = seq(5, 100, 5), anglesoi = seqClosed(0, 2 * pi, 24), nsamples = 1e+05, bw = 20, mc.cores = getOption("mc.cores", default = 1))transformBarycentric. Will use the z column as test statistic, or if this column is not given the r column
nsamples is high enough
backmodels
n
n a second list containing:
anglesoi, these weights will be used to calculate the p-value
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 1
barycoords = transformBarycentric(Eoi)
hist(barycoords$angle)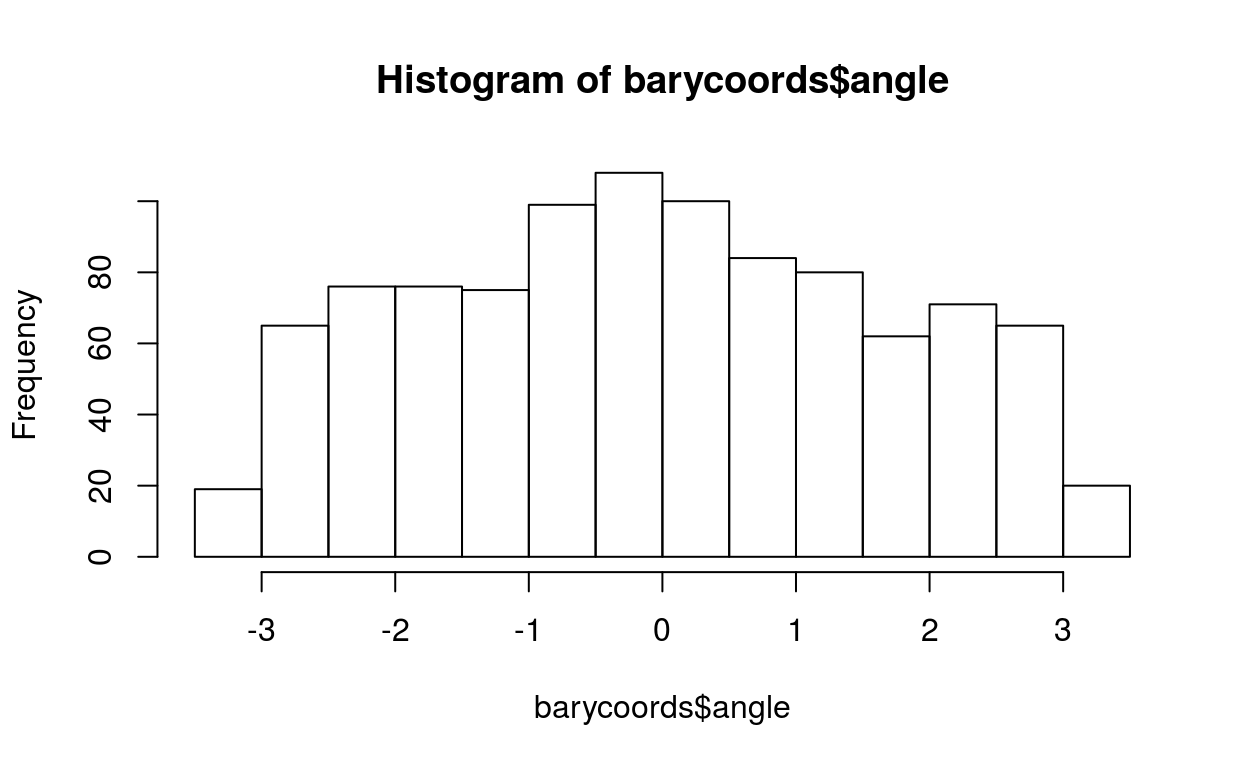
bm = generateBackgroundModel(barycoords)
# the distribution of mean angle of the samples is not uniform due to the non-uniform distribution of the angles of individual genes
hist(bm$backmodels[[1]]$angles)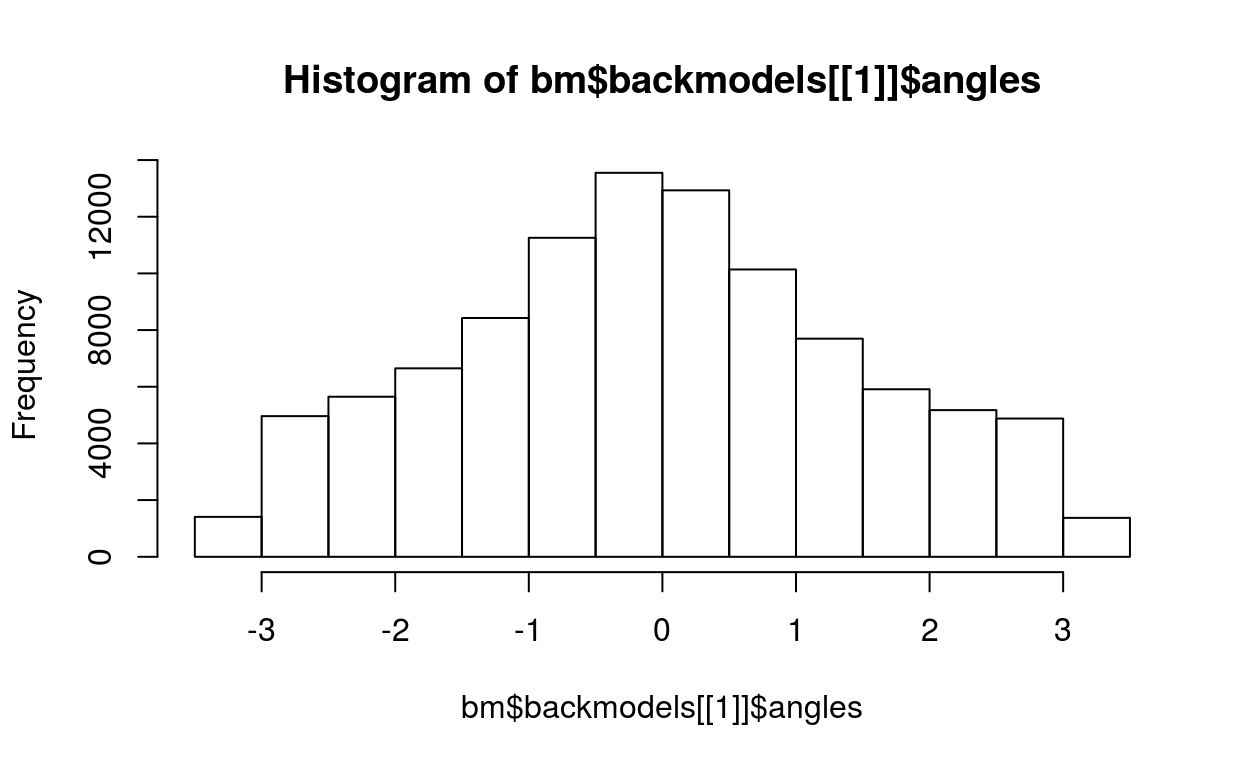
# the whole distribution (and therefore also the p-value) also depends on the mean angle
plotdata = data.frame(angle = cut(bm$backmodels[[1]]$angles, 10), z = bm$backmodels[[1]]$z)
ggplot2::ggplot(plotdata) + ggplot2::geom_violin(ggplot2::aes(angle, z))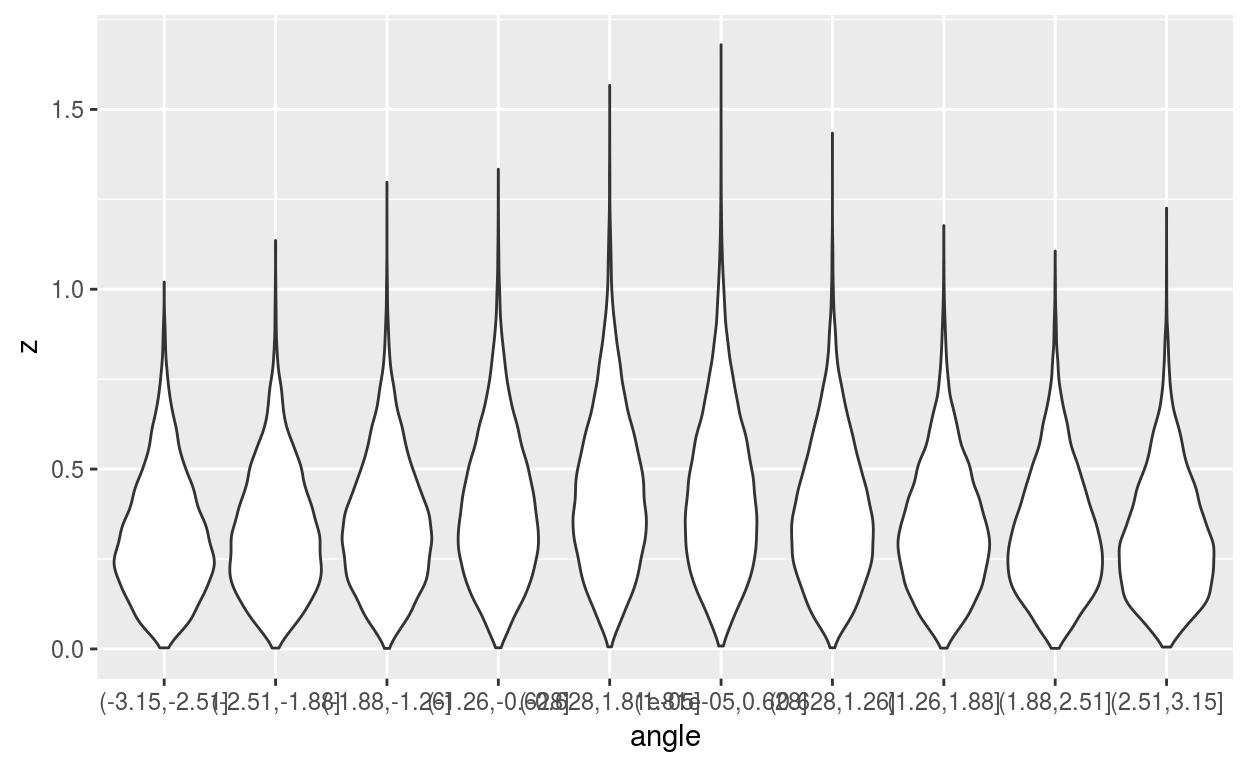
testRayleigh(angles)
testRayleigh(as.numeric(circular::rvonmises(10, circular::circular(1), 2)))## [1] 0.004219547testRayleigh(seq(0, 2*pi, 0.1))## [1] 0.9995545
Wrapper around the mgsa method
estimateRedundancy(scores, gsets, Gdiffexp)testUnidirectionality() containing the filtered enrichment scores for every gene set
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 4 # the first 100 genes are more upregulated in the first condition
barycoords = transformBarycentric(Eoi)
Gdiffexp = (1:1000)[barycoords$r > 1]
gsets = list(a=1:50, b=c(1:50, 100:110), c=200:500) # a and b are redundant, but a is stronger enriched
scores = testUnidirectionality(barycoords, gsets, Gdiffexp=(1:1000)[barycoords$r > 1])
scores$redundancy = estimateRedundancy(scores, gsets, Gdiffexp)
scores[scores$gsetid == "a", "redundancy"] > scores[scores$gsetid == "b", "redundancy"]## [1] TRUEtestEnrichment(Goi, gsets, background, minknown = 2, mindiffexp = 2, maxknown = 500)
Goi = 1:50
gsets = list(a= 20:70, b = 45:80)
background = 1:100
testEnrichment(Goi, gsets, background)## pval odds found gsetid qval
## 1 0.02246197 2.4248312 31 a 0.04492393
## 2 0.99999997 0.0934603 6 b 0.99999997Tests for local upregulation locally in certain directions
testLocality(Goi, Gdiffexp, angles, deltangle = pi/24, bandwidth = pi/3)transformBarycentric
Eoi = matrix(rnorm(1000*3, sd=0.5), 1000, 3, dimnames=list(1:1000, c(1,2,3)))
Eoi[1:100,1] = Eoi[1:100,1] + 4 # the first 100 genes are more upregulated in the first condition
barycoords = transformBarycentric(Eoi)
Goi = 1:50
qvals = testLocality(Goi, Gdiffexp=(1:1000)[barycoords$r > 1], barycoords)
plot(attr(qvals, "anglesoi"), qvals)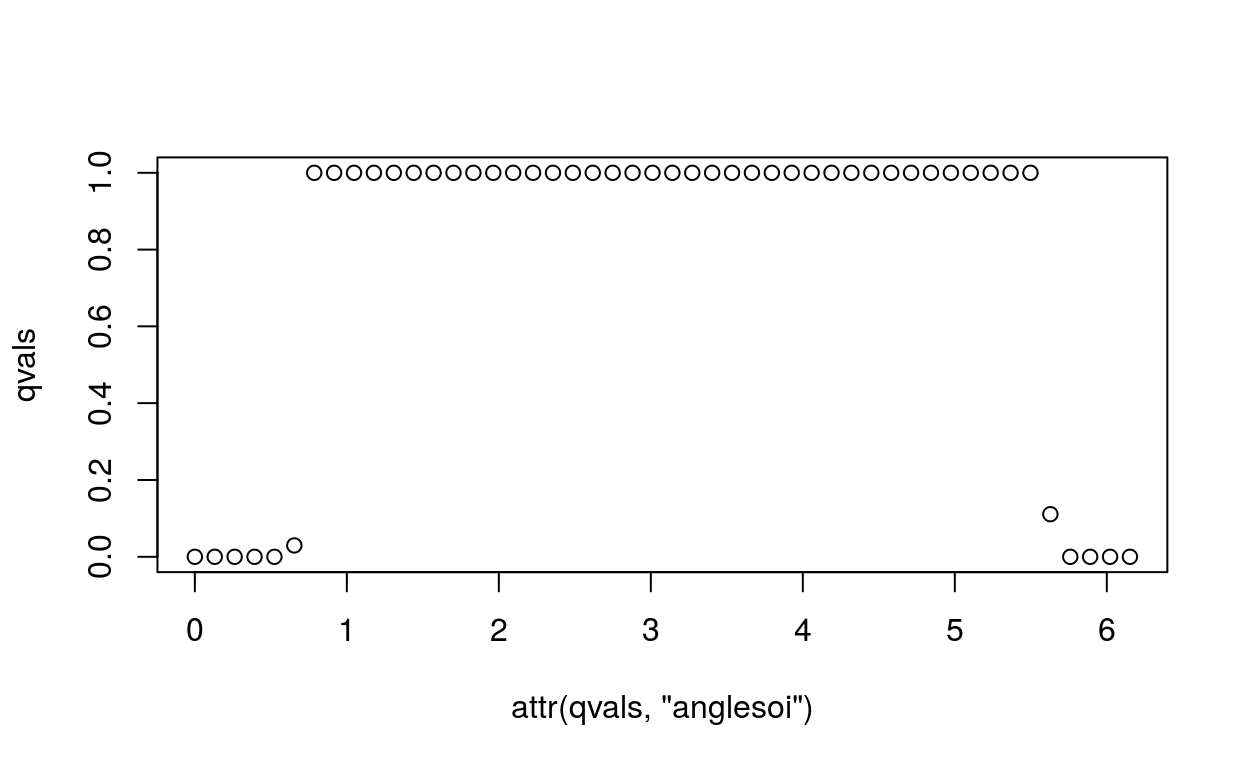
This dataset contains, among others, gene expression data from the three main macrophage progenitor populations in mice. Note that due to size restrictions of Bioconductor, half of non-differentially expressed genes are not included in the dataset.
vandelaar
An object of class ExpressionSet with 11679 rows and 24 columns.
https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE76999